
Przestrzeń i wymiar wektora bazowego, aksjomaty, własności
ZA przestrzeń wektorowa jest niepustym zestawem V= lub, v, w,…, których elementami są wektory. Przeprowadzane są z nimi ważne operacje, wśród których wyróżniają się:
- Suma między dwoma wektorami u + v co powoduje z, który należy do zestawu V.
- Mnożenie liczby rzeczywistej α przez wektor v: α v co daje inny wektor Y który należy do V.

Aby oznaczyć wektor, używamy pogrubienia (v jest wektorem), a dla skalarów lub liczb litery greckie (α to liczba).
Indeks artykułów
- 1 Aksjomaty i własności
- 2 Przykłady przestrzeni wektorowych
- 2.1 Przykład 1
- 2.2 Przykład 2
- 2.3 Przykład 3
- 2.4 Przykład 4
- 3 Baza i wymiar przestrzeni wektorowej
- 3.1 Baza
- 3.2 Wymiar
- 3.3 Podprzestrzeń wektorowa
- 4 ćwiczenia rozwiązane
- 4.1 - Ćwiczenie 1
- 4.2 - Ćwiczenie 2
- 4.3 - Ćwiczenie 3
- 5 Referencje
Aksjomaty i własności
Aby uzyskać przestrzeń wektorową, należy spełnić osiem następujących aksjomatów:
1-przełączane: lub +v = v +lub
2-przechodniość: (lub + v) + w = lub + ( v + w)
3-Istnienie wektora zerowego 0 takie że 0 + v = v
4-Istnienie przeciwieństwa: przeciwieństwo v to jest (-v) , tak jak v + (-v) = 0
5-Dystrybucja iloczynu względem sumy wektorów: α ( lub + v ) = αlub +αv
6-Dystrybucja iloczynu ze względu na sumę skalarną: (α + β)v = αv +βv
7-Łączność iloczynu skalarnego: α (β v) = (α β)v
8-liczba 1 jest elementem neutralnym, ponieważ: 1v = v
Przykłady przestrzeni wektorowych
Przykład 1
Wektory w płaszczyźnie (R²) są przykładem przestrzeni wektorowej. Wektor na płaszczyźnie to obiekt geometryczny, który ma zarówno wielkość, jak i kierunek. Jest reprezentowany przez zorientowany segment, który należy do wspomnianej płaszczyzny i którego rozmiar jest proporcjonalny do jego wielkości.
Suma dwóch wektorów na płaszczyźnie może być zdefiniowana jako operacja przesunięcia geometrycznego drugiego wektora po pierwszym. Wynikiem sumy jest zorientowany segment, który zaczyna się od początku pierwszego i dochodzi do końca drugiego.
Na rysunku widać, że suma w R² jest przemienna.
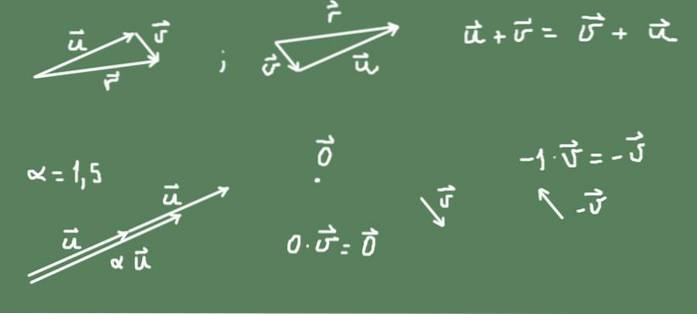
Zdefiniowano również iloczyn liczby α i wektora. Jeśli liczba jest dodatnia, kierunek pierwotnego wektora jest zachowany, a rozmiar jest α razy większy od pierwotnego wektora. Jeśli liczba jest ujemna, kierunek jest odwrotny, a rozmiar wektora wynikowego jest wartością bezwzględną liczby.
Wektor przeciwny do dowolnego wektora v to jest -v = (- 1) v.
Wektor zerowy jest punktem na płaszczyźnie R², a liczba zero razy wektor daje wektor zerowy.
Wszystko, co zostało powiedziane, zilustrowano na rysunku 2.
Przykład 2
Zestaw P. wszystkich wielomianów stopnia mniejszego lub równego dwa, w tym stopnia zero, tworzą zbiór, który spełnia wszystkie aksjomaty przestrzeni wektorowej.
Niech wielomian P (x) = a x² + b x + c i Q (x) = d x² + e x + f
Suma dwóch wielomianów jest zdefiniowana: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
Suma wielomianów należących do zbioru P. jest przemienna i przechodnia.
Null wielomian należący do zestawu P. to taki, który ma wszystkie współczynniki równe zero:
0 (x) = 0 x² + 0 x + 0
Suma skalara α przez wielomian jest definiowana jako: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
Odwrotny wielomian P (x) to -P (x) = (-1) P (x).
Z powyższego wynika, że zestaw P. ze wszystkich wielomianów stopnia mniejszego lub równego dwa, jest przestrzenią wektorową.
Przykład 3
Zestaw M wszystkich macierzy m wierszy x n kolumn, których elementy są liczbami rzeczywistymi, tworzy rzeczywistą przestrzeń wektorową, w odniesieniu do operacji dodawania macierzy i iloczynu liczby przez macierz.
Przykład 4
Zbiór F funkcji ciągłych zmiennej rzeczywistej tworzy przestrzeń wektorową, ponieważ można zdefiniować sumę dwóch funkcji, mnożenie skalara przez funkcję, funkcję zerową i funkcję symetryczną. Spełniają również aksjomaty charakteryzujące przestrzeń wektorową.
Baza i wymiar przestrzeni wektorowej
Baza
Podstawę przestrzeni wektorowej definiuje się jako zbiór liniowo niezależnych wektorów, tak że z ich liniowej kombinacji można wygenerować dowolny wektor tej przestrzeni wektorowej.
Liniowe łączenie dwóch lub więcej wektorów polega na pomnożeniu wektorów przez pewną wartość skalarną, a następnie dodaniu ich wektorowo.
Na przykład w przestrzeni wektorowej wektorów w trzech wymiarach utworzonej przez R3, używana jest podstawa kanoniczna zdefiniowana przez wektory jednostkowe (o wielkości 1) ja, jot, k.
Gdzie ja = (1, 0, 0); jot = (0, 1, 0); k = (0, 0, 1). Są to wektory kartezjańskie lub kanoniczne.
Dowolny wektor V należący do R³ jest zapisywany jako V = a ja + b jot + do k, która jest liniową kombinacją wektorów bazowych ja, jot, k. Skalary lub liczby a, b, c są znane jako składowe kartezjańskie V.
Mówi się również, że wektory bazowe przestrzeni wektorowej tworzą generator przestrzeni wektorowej.
Wymiar
Wymiar przestrzeni wektorowej jest liczbą kardynalną bazy wektorowej tej przestrzeni; to znaczy liczba wektorów, które tworzą wspomnianą podstawę.
Ten kardynał to maksymalna liczba liniowo niezależnych wektorów tej przestrzeni wektorowej, a jednocześnie minimalna liczba wektorów tworzących zespół generatora tej przestrzeni.
Bazy przestrzeni wektorowej nie są unikalne, ale wszystkie bazy tej samej przestrzeni wektorowej mają ten sam wymiar.
Podprzestrzeń wektorowa
Podprzestrzeń wektorowa S przestrzeni wektorowej V jest podzbiorem V, w którym te same operacje są zdefiniowane jak w V i spełnia wszystkie aksjomaty przestrzeni wektorowej. Dlatego podprzestrzeń S będzie również przestrzenią wektorową.
Przykładem podprzestrzeni wektorowej są wektory należące do płaszczyzny XY. Ta podprzestrzeń jest podzbiorem wektorowej przestrzeni wymiarowości większej niż zbiór wektorów należących do trójwymiarowej przestrzeni XYZ.
Inny przykład podprzestrzeni wektorowej S1 przestrzeni wektorowej S utworzonej przez wszystkie macierze 2 × 2 z elementami rzeczywistymi jest zdefiniowany poniżej:
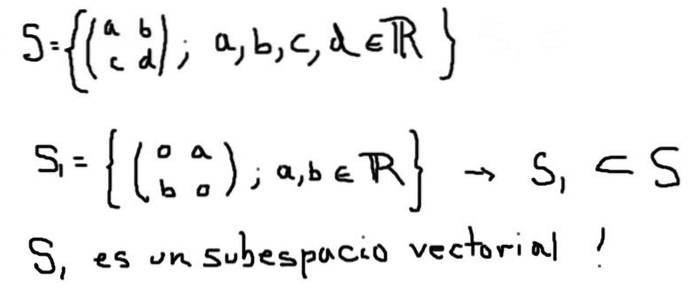
Z drugiej strony, S2 zdefiniowana poniżej, chociaż jest podzbiorem S, nie tworzy wektorowej podprzestrzeni:

Rozwiązane ćwiczenia
-Ćwiczenie 1
Niech wektory będą V1= (1, 1, 0); V2= (0, 2, 1) i V3= (0, 0, 3) w R3.
a) Pokaż, że są liniowo niezależne.
b) Pokaż, że tworzą podstawę w R3, ponieważ każda trójka (x, y, z) może być zapisana jako liniowa kombinacja V1, V2, V3.
c) Znajdź składniki potrójnej V = (-3,5,4) u podstawy V1, V2, V3.
Rozwiązanie
Kryterium wykazania liniowej niezależności polega na ustaleniu następującego zestawu równań w α, β i γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
W przypadku, gdy jedynym rozwiązaniem tego układu jest α = β = γ = 0, to wektory są liniowo niezależne, w przeciwnym razie nie są.
Aby otrzymać wartości α, β i γ, proponujemy następujący układ równań:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
Pierwsza prowadzi do α = 0, druga α = -2 ∙ β, ale ponieważ α = 0 to β = 0. Trzecie równanie implikuje, że γ = (- 1/3) β, ale ponieważ β = 0, to γ = 0.
Odpowiedz
Stwierdzono, że jest to zbiór liniowo niezależnych wektorów w R3 .
Odpowiedź b
Teraz zapiszmy potrójną (x, y, z) jako liniową kombinację V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Gdzie masz:
α = x
α + 2 β = y
β + 3 γ = z
Pierwsza oznacza α = x, druga β = (y-x) / 2, a trzecia γ = (z- y / 2 + x / 2) / 3. W ten sposób znaleźliśmy generatory α, β i γ dowolnej trójki R3
Odpowiedź c
Przejdźmy dalej, aby znaleźć składniki potrójnej V = (-3,5,4) u podstawy V1, V2, V3.
Zastępujemy odpowiednie wartości w wyrażeniach znalezionych powyżej dla generatorów.
W tym przypadku mamy: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4- 5/2 + (- 3) / 2) / 3 = 0
To jest:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Na koniec:
V = -3 V1 + 4 V2 + 0 V3
Kończymy to V1, V2, V3 tworzą podstawę w przestrzeni wektorowej R3 o wymiarze 3.
-Ćwiczenie 2
Wyraź wielomian P (t) = t² + 4t -3 jako liniową kombinację P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t i P3 (t) = t + 3.
Rozwiązanie
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
gdzie mają zostać określone liczby x, y, z.
Mnożenie i grupowanie wyrazów o tym samym stopniu w t daje:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
Co prowadzi nas do następującego układu równań:
x + 2y = 1
-2x -3y + z = 4
5x + 3 z = -3
Rozwiązania tego układu równań to:
x = -3, y = 2, z = 4.
To jest:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
-Ćwiczenie 3
Pokaż, że wektory v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) i v3= (2, 1, -1, 1) R⁴ są liniowo niezależne.
Rozwiązanie
Liniowo łączymy te trzy wektory v1, v2, v3 i żądamy, aby kombinacja dodała zerowy element R⁴
do v1 + b v2 + do v3 = 0
Mianowicie,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
To prowadzi nas do następującego układu równań:
a + b + 2 c = 0
b + c = 0
-a - c = 0
2 a + b + c = 0
Odejmując pierwszą i czwartą otrzymujemy: -a + c = 0, co implikuje a = c.
Ale jeśli spojrzymy na trzecie równanie, otrzymamy a = -c. Jedynym sposobem, w jaki a = c = (- c) zachodzi, jest to, że c wynosi 0, a zatem a będzie również równe 0.
a = c = 0
Jeśli podstawimy ten wynik w pierwszym równaniu, to wnioskujemy, że b = 0.
Wreszcie a = b = c = 0, więc można wywnioskować, że wektory v1, v2 i v3 są liniowo niezależne.
Bibliografia
- Lipschutz, S. 1993. Algebra liniowa. Druga edycja. McGraw-Hill. 167 - 198.
Jeszcze bez komentarzy