
Twierdzenie Czebyszowa, co to jest, zastosowania i przykłady
Plik Twierdzenie Czebyszowa (lub nierówność Czebyszowa) jest jednym z najważniejszych klasycznych wyników teorii prawdopodobieństwa. Pozwala oszacować prawdopodobieństwo zdarzenia opisanego w kategoriach zmiennej losowej X, dostarczając nam granicę, która nie zależy od rozkładu zmiennej losowej, ale od wariancji X.
Twierdzenie zostało nazwane na cześć rosyjskiego matematyka Pafnuty Chebyshova (również pisanego jako Chebychev lub Tchebycheff), który, mimo że nie był pierwszym, który sformułował twierdzenie, był pierwszym, który dał dowód w 1867 r..

Ta nierówność lub te, które ze względu na swoje cechy nazywane są nierównościami Czebyszowa, służy głównie do przybliżania prawdopodobieństw poprzez obliczanie granic.
Indeks artykułów
- 1 Co robi?
- 2 Zastosowania i przykłady
- 2.1 Ograniczanie prawdopodobieństw
- 2.2 Dowód twierdzeń granicznych
- 2.3 Wielkość próby
- 3 Nierówności typu Czebyszowa
- 4 Odnośniki
Z czego to się składa?
W badaniu teorii prawdopodobieństwa zdarza się, że znając funkcję rozkładu zmiennej losowej X, można obliczyć jej wartość oczekiwaną - lub oczekiwanie matematyczne E (X) - oraz jej wariancję Var (X), o ile takie wielkości istnieją . Jednak sytuacja odwrotna niekoniecznie jest prawdą..
Oznacza to, że znając E (X) i Var (X) niekoniecznie jest możliwe uzyskanie funkcji rozkładu X, dlatego takie wielkości jak P (| X |> k) dla niektórych k> 0 są bardzo trudne do uzyskania. Ale dzięki nierówności Czebyszowa można oszacować prawdopodobieństwo zmiennej losowej.
Twierdzenie Czebyszowa mówi nam, że jeśli mamy zmienną losową X na przestrzeni próbkowania S z funkcją prawdopodobieństwa p, a jeśli k> 0, to:
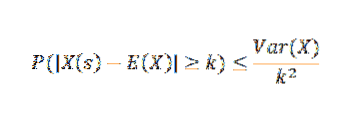
Zastosowania i przykłady
Wśród wielu zastosowań twierdzenia Czebyszowa można wymienić:
Ograniczające prawdopodobieństwa
Jest to najczęstsze zastosowanie i służy do określenia górnej granicy dla P (| X-E (X) | ≥k), gdzie k> 0, tylko z wariancją i oczekiwaniem zmiennej losowej X, bez znajomości funkcji prawdopodobieństwa.
Przykład 1
Załóżmy, że liczba produktów wytwarzanych w firmie w ciągu tygodnia jest zmienną losową, która wynosi średnio 50.
Jeśli wiadomo, że wariancja tygodnia produkcji jest równa 25, to cóż możemy powiedzieć o prawdopodobieństwie, że w tym tygodniu produkcja różni się o więcej niż 10 od średniej?
Rozwiązanie
Stosując nierówność Czebyszowa mamy:
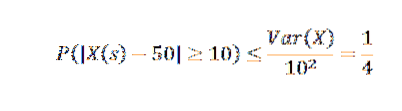
Z tego możemy uzyskać, że prawdopodobieństwo, że w tygodniu produkcyjnym liczba artykułów przewyższa średnią o więcej niż 10, wynosi co najwyżej 1/4.
Dowód twierdzeń granicznych
Nierówność Czebyszowa odgrywa ważną rolę w dowodzeniu najważniejszych twierdzeń granicznych. Jako przykład mamy:
Słabe prawo wielkich liczb
Prawo to ustanawia, że biorąc pod uwagę ciąg X1, X2,…, Xn,… niezależnych zmiennych losowych o tym samym rozkładzie średniej E (Xi) = μ i wariancji Var (X) = σdwa, i znaną średnią próbkę:
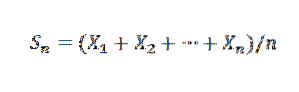
Wtedy dla k> 0 mamy:
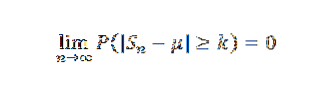
Lub równoważnie:
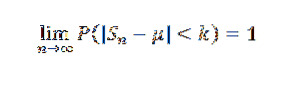
Demonstracja
Najpierw zwróćmy uwagę na następujące kwestie:
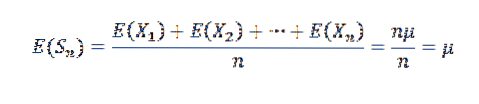
Ponieważ X1, X2,…, Xn są niezależne, wynika z tego, że:
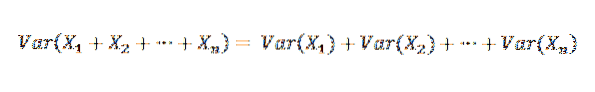
W związku z tym można stwierdzić, co następuje:
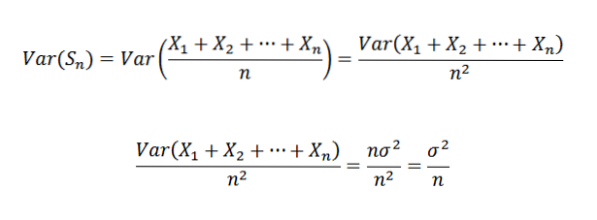
Następnie, korzystając z twierdzenia Czebyszowa, mamy:
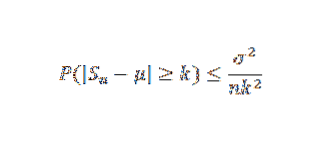
Wreszcie twierdzenie wynika z faktu, że granica po prawej stronie wynosi zero, gdy n dąży do nieskończoności.
Należy zauważyć, że test ten został wykonany tylko dla przypadku, w którym istnieje wariancja Xi; to znaczy nie rozchodzi się. Zatem obserwujemy, że twierdzenie jest zawsze prawdziwe, jeśli istnieje E (Xi).
Twierdzenie graniczne Czebyszowa
Jeśli X1, X2,…, Xn,… jest ciągiem niezależnych zmiennych losowych, takim, że istnieje jakieś C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
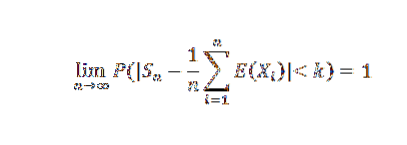
Demonstracja
Ponieważ sekwencja wariancji jest jednolicie ograniczona, mamy Var (Sn) ≤ C / n, dla wszystkich naturalnych n. Ale wiemy, że:
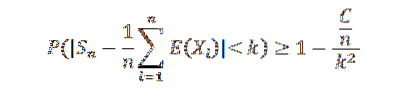
Sprawiając, że n dąży do nieskończoności, następujące wyniki:
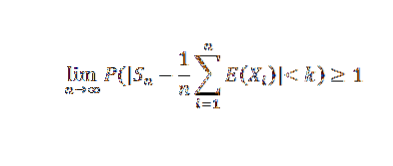
Ponieważ prawdopodobieństwo nie może przekroczyć wartości 1, uzyskuje się pożądany wynik. W konsekwencji tego twierdzenia możemy wspomnieć o szczególnym przypadku Bernoulliego.
Jeśli eksperyment jest powtarzany n razy niezależnie z dwoma możliwymi wynikami (niepowodzeniem i sukcesem), gdzie p jest prawdopodobieństwem sukcesu w każdym eksperymencie, a X jest zmienną losową reprezentującą liczbę uzyskanych sukcesów, to dla każdego k> 0 masz do:
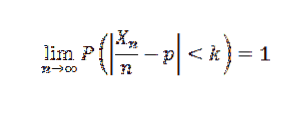
Wielkość próbki
Jeśli chodzi o wariancję, nierówność Czebyszowa pozwala nam znaleźć próbkę o wielkości n, która jest wystarczająca do zagwarantowania, że prawdopodobieństwo wystąpienia | Sn-μ |> = k jest tak małe, jak to pożądane, co pozwala nam uzyskać przybliżenie do średni.
Dokładnie, niech X1, X2,… Xn będzie próbką niezależnych zmiennych losowych o rozmiarze n i załóżmy, że E (Xi) = μ i jej wariancja σdwa. Tak więc, według nierówności Czebyszowa, mamy:
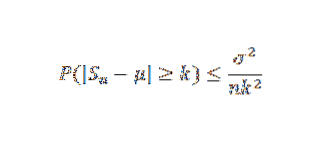
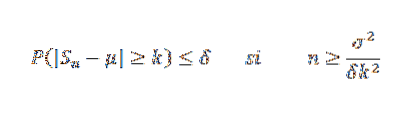
Przykład
Załóżmy, że X1, X2,… Xn są próbką niezależnych zmiennych losowych z rozkładem Bernoulliego, tak że przyjmują wartość 1 z prawdopodobieństwem p = 0,5.
Jaka powinna być wielkość próby, aby była w stanie zagwarantować, że prawdopodobieństwo, że różnica między średnią arytmetyczną Sn a jej wartością oczekiwaną (przekraczającą o więcej niż 0,1) jest mniejsze lub równe 0., 01?
Rozwiązanie
Mamy, że E (X) = μ = p = 0,5 i że Var (X) = σdwa= p (1-p) = 0,25. Z nierówności Czebyszowa, dla każdego k> 0 mamy:
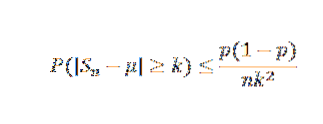
Teraz, biorąc k = 0,1 i δ = 0,01, mamy:
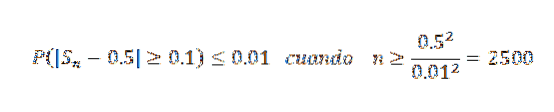
W ten sposób stwierdza się, że potrzebna jest próba o wielkości co najmniej 2500, aby zagwarantować, że prawdopodobieństwo zdarzenia | Sn - 0,5 |> = 0,1 jest mniejsze niż 0,01.
Nierówności typu Czebyszowa
Istnieje kilka nierówności związanych z nierównościami Czebyszowa. Jedną z najbardziej znanych jest nierówność Markowa:
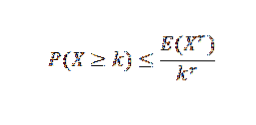
W tym wyrażeniu X jest nieujemną zmienną losową z k, r> 0.
Nierówność Markowa może przybierać różne formy. Na przykład niech Y będzie nieujemną zmienną losową (więc P (Y> = 0) = 1) i załóżmy, że istnieje E (Y) = μ. Przypuśćmy też, że (E (Y))r= μr istnieje dla pewnej liczby całkowitej r> 1. Następnie:
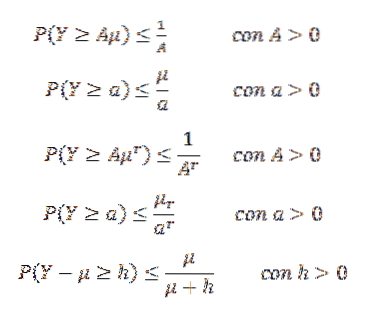
Inną nierównością jest Gaussian, który mówi nam, że mając unimodalną zmienną losową X z trybem równym zero, to dla k> 0,
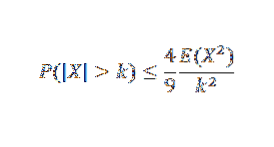
Bibliografia
- Kai Lai Chung. Elementarna teoria proability z procesami stochastycznymi. Springer-Verlag New York Inc.
- Kenneth.H. Rosen, matematyka dyskretna i jej zastosowania. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Prawdopodobieństwo i aplikacje statystyczne. S. A. MEKSYKAŃSKA ALHAMBRA.
- Dr Seymour Lipschutz 2000 Rozwiązane problemy matematyki dyskretnej. McGRAW-HILL.
- Dr Seymour Lipschutz Problemy teorii i prawdopodobieństwa. McGRAW-HILL.


Jeszcze bez komentarzy