
Właściwości transformaty Fouriera, zastosowania, przykłady
Plik Przekształcenie Fouriera to metoda analitycznej adekwatności zorientowana na funkcje całkowalne należące do rodziny tintegralnie przekształcony. Polega na przedefiniowaniu funkcji fa (t) pod względem Cos (t) i Sen (t).
Tożsamości trygonometryczne tych funkcji, wraz z ich wyprowadzeniem i charakterystyką anty-pierwotną, służą do zdefiniowania transformaty Fouriera poprzez następującą złożoną funkcję:
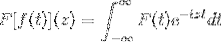
Co jest prawdą, o ile wyrażenie ma sens, to znaczy, gdy całka niewłaściwa jest zbieżna. Algebraicznie mówi się, że transformata Fouriera jest liniowym homeomorfizmem.
Każda funkcja, nad którą można pracować z transformacją Fouriera, musi mieć wartość null poza zdefiniowanym parametrem.
Indeks artykułów
- 1 Właściwości
- 1.1 Istnienie
- 1.2 Liniowość transformacji Fouriera
- 1.3 Transformacja Fouriera pochodnej
- 1.4 Zróżnicowanie transformaty Fouriera
- 1.5 Transformacja Fouriera tłumaczenia
- 1.6 Tłumaczenie transformaty Fouriera
- 1.7 Transformacja Fouriera grupy skali
- 1.8 Symetria
- 1.9 Transformacja Fouriera iloczynu splotu
- 1.10 Ciągłość i rozpad w nieskończoność
- 2 Historia
- 3 Do czego służy transformata Fouriera?
- 3.1 Szereg Fouriera
- 3.2 Inne postacie szeregu Fouriera
- 4 Aplikacje
- 4.1 Obliczanie rozwiązania podstawowego
- 4.2 Teoria sygnałów
- 5 przykładów
- 5.1 Przykład 1
- 5.2 Przykład 2
- 6 Proponowane ćwiczenia
- 7 Referencje
Nieruchomości

Transformacja Fouriera spełnia następujące właściwości:
Istnienie
Aby zweryfikować istnienie transformaty Fouriera w funkcji f (t) zdefiniowanej w liczbach rzeczywistych R, muszą zostać spełnione następujące 2 aksjomaty:
- f (t) jest ciągłe dla wszystkiego R
- f (t) jest integrowalna w R
Liniowość transformacji Fouriera
Niech M (t) i N (t) będą dowolnymi dwiema funkcjami z określonymi transformatami Fouriera, z dowolnymi stałymi a i b.
fa [a M (t) + b N (t)] (z) = a fa [M (t)] (z) + b fa [N (t)] (z)
Co jest również wspierane przez liniowość całki o tej samej nazwie.
Transformacja Fouriera pochodnej
Ma funkcję fa który jest ciągły i całkowalny we wszystkich liczbach rzeczywistych, gdzie:
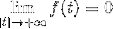
I pochodna f (f ') jest ciągły i określony fragmentarycznie R
Przekształcenie Fouriera pochodnej jest zdefiniowane przez całkowanie przez części, za pomocą następującego wyrażenia:
fa [f '(t)] (z) = izfa [f (t)] (z)
W wyprowadzeniach wyższego rzędu zostanie zastosowany w sposób homologiczny, gdzie dla wszystkich n 1 mamy:
fa [fa n'(t)] (z) = (iz)nfa [f (t)] (z)
Różniczkowanie przez transformację Fouriera
Ma funkcję fa który jest ciągły i całkowalny we wszystkich liczbach rzeczywistych, gdzie:
ja (d / dz)fa [f (t)] (z) = fa [t. f (t)] (z)
Przekształcenie Fouriera tłumaczenia
Dla wszystkich θ który należy do zbioru S i T który należy do zbioru S ', mamy:
F [ τdo θ] = i-iay fa [ θ] F [ τdoT ] = i-iax fa [ T]
Z τdo pracując jako operator translacji na wektorze a.
Tłumaczenie transformaty Fouriera
Dla wszystkich θ który należy do zbioru S i T który należy do zbioru S ', mamy:
τdo fa [θ] = fa [i-iax.θ] τdo F [T ] = fa [i-iay . T]
Dla wszystkich do który należy do R
Transformacja Fouriera grupy skalowej
Dla wszystkich θ który należy do zbioru S. T który należy do zbioru S '
λ należeć do R - 0 musisz:
fa [θ (λx)] = (1 / | λ |) fa [θ] (Y /λ)
fa [T (λx)] = (1 / | λ |) fa [T] (y / λ)
tak fa jest funkcją ciągłą i wyraźnie integrowalną, gdzie a> 0. Wtedy:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Aby zademonstrować ten wynik, możemy przejść do zmiany zmiennej.
Kiedy T → +, to s = w → + ∞
Gdy T → - to s = w → - ∞
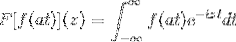
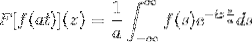
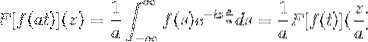
Symetria
Aby zbadać symetrię transformaty Fouriera, należy zweryfikować tożsamość wzoru Parsevala i Plancherela.
Mamy θ i δ, które należą do S. Stamtąd można wywnioskować, że:
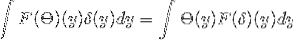
Dostaję
1 / (2π)re F [θ ], F [δ] Tożsamość Parsevala
1 / (2π)d / 2 || F [θ ] ||LdwaRre Formuła Plancherela
Przekształcenie Fouriera iloczynu splotu
Dążąc do podobnych celów, jak w transformacie Laplace'a, splot funkcji odnosi się do iloczynu między ich transformatami Fouriera.
Mamy f i g jako 2 ograniczone, określone i całkowicie integrowalne funkcje:
F (f * g) = F (f). F (g)
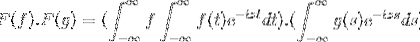
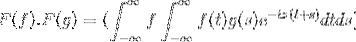
Następnie przy zmianie zmiennej
t + s = x; kontynuuje z niewłaściwą podwójną całką
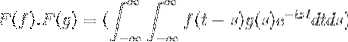
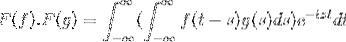
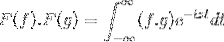
F (f). F (g) = F (f. G)
Ciągłość i upadek w nieskończoność
Dla wszystkich θ który należy do R, F [ θ] spełnia kryteria funkcji ciągłej ograniczonej w Rre.
Również F [ θ] (y) → 0 w C jeśli | y | → ∞
Fabuła
Ta matematyczna koncepcja została przedstawiona przez Josepha B. Fouriera w 1811 r. Podczas opracowywania traktatu o rozprzestrzenianie się ciepła. Szybko został przyjęty przez różne gałęzie nauki i inżynierii.
Ustanowiono go jako główne narzędzie pracy w badaniu równań z pochodnymi cząstkowymi, a nawet porównując je z istniejącym stosunkiem pracy między Transformata Laplace'a i równania różniczkowe zwyczajne.
Do czego służy transformata Fouriera?
Służy przede wszystkim do znacznego uproszczenia równań, przy przekształcaniu wyrażeń pochodnych na elementy potęgowe, oznaczając wyrażenia różniczkowe w postaci całkowalnych wielomianów..
W optymalizacji, modulacji i modelowaniu wyników działa jak znormalizowane wyrażenie, będące częstym źródłem informacji inżynierskich po kilku pokoleniach.
Szereg Fouriera
Są to szeregi zdefiniowane w kategoriach cosinusów i sinusów; Służą do ułatwienia pracy z ogólnymi funkcjami okresowymi. Po zastosowaniu stanowią część technik rozwiązywania zwykłych i cząstkowych równań różniczkowych..
Szeregi Fouriera są jeszcze bardziej ogólne niż szeregi Taylora, ponieważ rozwijają okresowe nieciągłe funkcje, które nie mają reprezentacji szeregów Taylora..
Inne formy szeregu Fouriera
Aby zrozumieć transformację Fouriera analitycznie, ważne jest, aby przejrzeć inne sposoby, w jakie można znaleźć szereg Fouriera, dopóki nie będziemy mogli zdefiniować szeregu Fouriera w jego złożonej notacji.
-Szeregi Fouriera na funkcji okresu 2L
Wielokrotnie konieczne jest dostosowanie struktury szeregu Fouriera do funkcji okresowych, których okres wynosi p = 2L> 0 w przedziale [-L, L].
-Szeregi Fouriera w funkcjach nieparzystych i parzystych
Uwzględniany jest przedział [-π, π], który zapewnia korzyści przy korzystaniu z symetrycznych charakterystyk funkcji.
Jeśli f jest parzyste, szereg Fouriera ustala się jako szereg cosinusów.
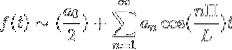
Jeśli f jest nieparzyste, szereg Fouriera ustala się jako szereg sinusów.
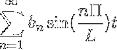
-Złożona notacja szeregu Fouriera
Jeśli mamy funkcję f (t), która spełnia wszystkie wymagania rozwijalności szeregu Fouriera, to można ją oznaczyć w przedziale [-t, t] używając jej złożonej notacji:
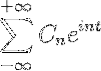
Aplikacje

Obliczanie rozwiązania podstawowego
Przekształcenie Fouriera jest potężnym narzędziem do badania równań różniczkowych cząstkowych typu liniowego o stałych współczynnikach. Odnoszą się one jednakowo do funkcji z nieograniczonymi domenami.
Podobnie jak transformata Laplace'a, transformata Fouriera przekształca pochodną funkcję częściową w zwykłe równanie różniczkowe, które jest znacznie prostsze w obsłudze..
Problem Cauchy'ego dla równania ciepła przedstawia pole częstego stosowania transformaty Fouriera, w której generowana jest funkcja rdzeń cieplny lub rdzeń Dirichleta.
Jeśli chodzi o obliczenia rozwiązania podstawowego, przedstawiono następujące przypadki, w których często znajduje się transformata Fouriera:
-Równanie Laplace'a
-Równanie ciepła
-Równanie Schrödingera
-Równanie falowe
Teoria sygnałów
Ogólny powód zastosowania transformaty Fouriera w tej gałęzi wynika głównie z charakterystycznej dekompozycji sygnału jako nieskończonej superpozycji łatwiejszych do leczenia sygnałów.
Może to być fala dźwiękowa lub fala elektromagnetyczna, transformata Fouriera wyraża to w postaci superpozycji fal prostych. Ta reprezentacja jest dość częsta w elektrotechnice.
Z drugiej strony istnieją przykłady zastosowania transformaty Fouriera w dziedzinie teorii sygnałów:
-Problemy z identyfikacją systemu. Założona f i g
-Problem ze spójnością sygnału wyjściowego
-Problemy z filtrowaniem sygnału
Przykłady
Przykład 1
Zdefiniuj transformatę Fouriera dla następującego wyrażenia:
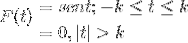
Możemy to również przedstawić w następujący sposób:
F (t) = Sen (t) [H.(t + k) - H.(t - k) ]
Prostokątny impuls jest zdefiniowany:
p (t) = H(t + k) - H.(t - k)
Przekształcenie Fouriera jest stosowane do następującego wyrażenia, które przypomina twierdzenie o modulacji.
f (t) = p (t) Sen (t)
Gdzie: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
A transformata Fouriera jest zdefiniowana przez:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Przykład 2
Zdefiniuj transformatę Fouriera dla wyrażenia:
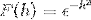
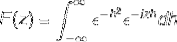
Ponieważ f (h) jest funkcją parzystą, można to stwierdzić
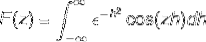
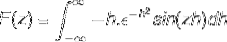
Całkowanie przez części jest stosowane przez wybranie zmiennych i ich różniczek w następujący sposób
u = sin (zh) du = z cos (zh) dh
dv = h (np-godz)dwa v = (np-godz)dwa / dwa
Zastępując masz
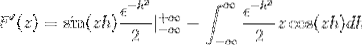
Po ocenie zgodnie z podstawowym twierdzeniem rachunku różniczkowego
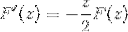
Stosując wcześniejszą wiedzę dotyczącą równań różniczkowych pierwszego rzędu, wyrażenie jest oznaczone jako
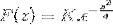
Aby otrzymać K, oceniamy
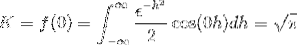
Wreszcie transformata Fouriera wyrażenia jest zdefiniowana jako
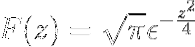
Proponowane ćwiczenia
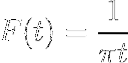
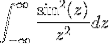
- Uzyskaj transformację wyrażenia W / (1 + wdwa)
Bibliografia
- Duoandikoetxea Zuazo, J., analiza Fouriera. Addison-Wesley Iberoamericana, Uniwersytet Autonomiczny w Madrycie, 1995.
- Lions, J. L., Analiza matematyczna i metody numeryczne w nauce i technologii. Springer-Verlag, 1990.
- Lieb, E.H., jądra Gaussa mają tylko maksymalizatory gaussowskie. Wymyślać. Matematyka. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier Series and Integrals. Academic Press, Nowy Jork, 1972.
- Schwartz, L., Théorie des Distributions. Ed Hermann, Paryż, 1966.



Jeszcze bez komentarzy