To ma macierz ortogonalna kiedy ta macierz pomnożona przez jej transpozycję daje w wyniku macierz tożsamości. Jeśli odwrotność macierzy jest równa transpozycji, to pierwotna macierz jest ortogonalna.
Macierze ortogonalne charakteryzują się tym, że liczba wierszy jest równa liczbie kolumn. Ponadto wektory wierszowe są jednostkowymi wektorami ortogonalnymi, a wektory wierszami transpozycji są również.
Kiedy macierz ortogonalna jest mnożona przez wektory przestrzeni wektorowej, to daje transformacja izometryczna, to znaczy transformacja, która nie zmienia odległości i zachowuje kąty.
Typowym przedstawicielem macierzy ortogonalnych są macierze rotacji. Nazywa się transformacje macierzy ortogonalnych w przestrzeni wektorowej przekształcenia ortogonalne.
Geometryczne transformacje obrotu i odbicia punktów reprezentowanych przez ich wektory kartezjańskie są przeprowadzane przez zastosowanie macierzy ortogonalnych na oryginalnych wektorach w celu uzyskania współrzędnych przekształconych wektorów. Z tego powodu macierze ortogonalne są szeroko stosowane w komputerowym przetwarzaniu grafiki..
Indeks artykułów
Tablica M jest ortogonalna, jeśli zostanie pomnożona przez transpozycję MT zwraca macierz jednostkową ja. Podobnie, iloczyn transpozycji macierzy ortogonalnej przez macierz oryginalną daje macierz identyczności:
M MT = MT M = ja
Konsekwencją poprzedniego stwierdzenia jest to, że transpozycja macierzy ortogonalnej jest równa jej macierzy odwrotnej:
MT = M-1.
Zbiór macierzy ortogonalnych wymiarów n x n tworzą grupę ortogonalną O (n). A podzbiór O (n) macierzy ortogonalnych z wyznacznikiem +1 z Grupa jednostkowych macierzy specjalnych SU (n). Macierze grup Słońce) to macierze, które powodują liniowe przekształcenia rotacji, znane również jako grupa rotacji.
Pokażmy, że macierz jest ortogonalna wtedy i tylko wtedy, gdy wektory wierszowe (lub wektory kolumnowe) są względem siebie ortogonalne io normie 1.
Załóżmy, że rzędy macierzy ortogonalnej n x n to n wektorów ortonormalnych o wymiarze n. Jeśli oznaczono v1, vdwa,…., Vn n wektorów jest spełnionych:
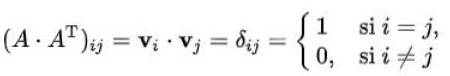
Gdzie jest oczywiste, że rzeczywiście zbiór wektorów wierszowych jest zbiorem wektorów ortogonalnych z normalnym.
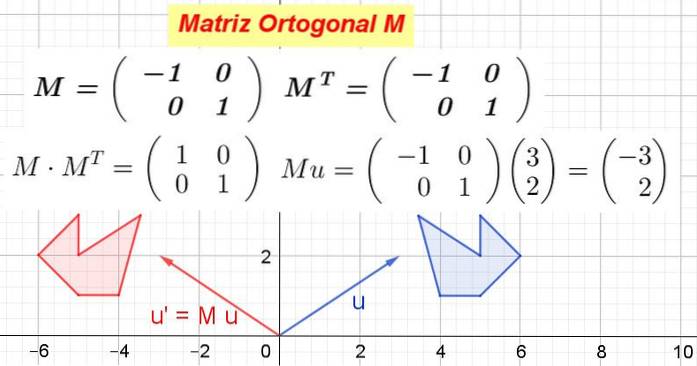
Pokaż, że macierz 2 x 2, która w pierwszym wierszu zawiera wektor v1= (-1 0), aw drugim rzędzie wektor v2= (0 1) jest macierzą ortogonalną.
Rozwiązanie: Macierz jest zbudowana M i obliczana jest jego transpozycja MT:
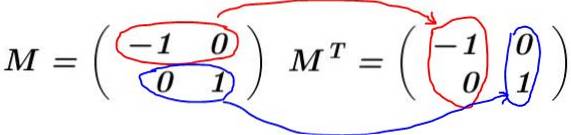
W tym przykładzie array M jest autotransponowany, to znaczy macierz i jej transpozycja są identyczne. Mnoży się M poprzez jego transpozycję MT:
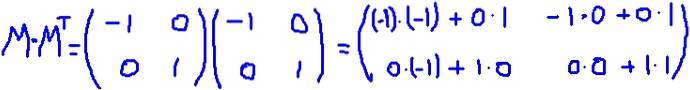
To jest potwierdzone M MT jest równa macierzy tożsamości:
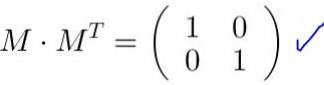
Gdy matrix M jest pomnożona przez współrzędne wektora lub punktu, uzyskuje się nowe współrzędne, które odpowiadają transformacji, jaką wykonuje macierz na wektorze lub punkcie.
Rysunek 1 pokazuje, jak to zrobić M przekształcić wektor lub na lub' a także jak M przekształć niebieski wielokąt w czerwony wielokąt. Co M jest ortogonalna, wtedy jest transformacją ortogonalną, która zachowuje odległości i kąty.
Załóżmy, że masz macierz 2 x 2 zdefiniowaną w liczbach rzeczywistych podanych przez następujące wyrażenie:
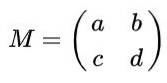
Znajdź prawdziwe wartości do, b, do Y re takie, że matrix M być macierzą ortogonalną.
Rozwiązanie: Z definicji macierz jest ortogonalna, jeśli pomnożona przez jej transpozycję otrzymana zostanie macierz tożsamości. Pamiętając, że transponowana macierz jest uzyskiwana z oryginału, zamieniając wiersze na kolumny, otrzymujemy następującą równość:
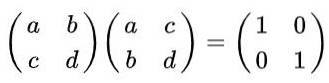
Wykonując mnożenie macierzy otrzymujemy:
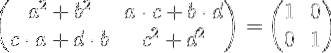
Porównując elementy lewej macierzy z elementami macierzy tożsamości po prawej, otrzymujemy układ czterech równań z czterema niewiadomymi a, b, c i d.
Proponujemy następujące wyrażenia dla a, b, c i d pod względem stosunków trygonometrycznych sinus i cosinus:
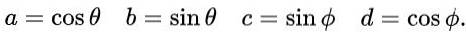
Dzięki tej propozycji i ze względu na podstawową tożsamość trygonometryczną, pierwsze i trzecie równanie są automatycznie spełnione w równości elementów macierzy. Trzecie i czwarte równanie są takie same iw równości macierzowej po podstawieniu proponowanych wartości wygląda to tak:
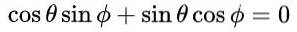
co prowadzi do następującego rozwiązania:
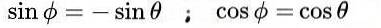
Ostatecznie otrzymujemy następujące rozwiązania dla macierzy ortogonalnej M:
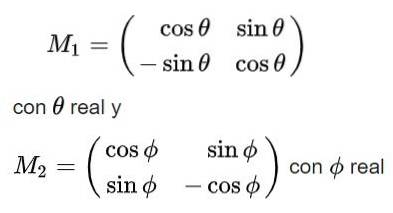
Zauważ, że pierwsze z rozwiązań ma wyznacznik +1, a więc należy do grupy SU (2), podczas gdy drugie rozwiązanie ma wyznacznik -1 i dlatego nie należy do tej grupy.
Biorąc pod uwagę następującą macierz, znajdź wartości a i b, aby otrzymać macierz ortogonalną.
Rozwiązanie: Aby dana macierz była ortogonalna, iloczyn z jej transpozycją musi być macierzą tożsamości. Następnie wykonywany jest iloczyn macierzy danej macierzy z jej transponowaną macierzą, dając następujący wynik:
Następnie wynik jest utożsamiany z macierzą tożsamości 3 x 3:
W drugim rzędzie trzecia kolumna mamy (a b = 0), ale do nie może być równe zero, ponieważ jeśli tak, to równość elementów drugiego rzędu i drugiej kolumny nie byłaby spełniona. Wtedy koniecznie b = 0. Zastępowanie b dla wartości 0 mamy:
Następnie równanie zostaje rozwiązane: 2a ^ 2 = 1, których rozwiązania to: + ½√2 i -½√2.
Biorąc pozytywne rozwiązanie dla do otrzymujemy następującą macierz ortogonalną:
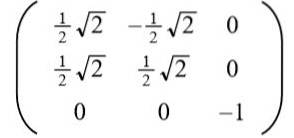
Czytelnik może łatwo sprawdzić, czy wektory wierszowe (a także wektory kolumnowe) są ortogonalne i unitarne, to znaczy ortonormalne.
Udowodnij, że matrix DO których są wektory wierszowe v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0–1) jest macierzą ortogonalną. Dodatkowo dowiedz się, jak przekształcane są wektory podstawy kanonicznej I J K do wektorów u1, u2 Y u3.
Rozwiązanie: Należy pamiętać, że element (i, j) macierzy pomnożony przez jej transpozycję jest iloczynem skalarnym wektora wiersza (i) i kolumny (j) transpozycji. Ponadto iloczyn ten jest równy delcie Kroneckera w przypadku, gdy macierz jest ortogonalna:
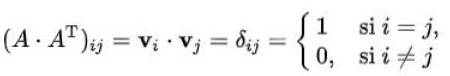
W naszym przypadku wygląda to tak:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Za pomocą którego pokazano, że jest to macierz ortogonalna.
Co więcej u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) i na koniec u3 = A k = (0, 0, -1)
Jeszcze bez komentarzy